使用comsol模拟水的沸腾

介绍

沸腾流动是第一类相变的一个例子，它可以通过将液体的温度提高到饱和温度以上来产生。实现这一点的方法有很多，最常见的两种方法是将外部热流施加到与液体接触的固体表面，或者通过降低周围环境中的压力来实现。加热表面引起的沸腾有三种截然不同的状态：成核、过渡和薄膜。沸腾状态取决于过热度和施加到表面的热通量的大小。过热度定义为固体表面温度与液体饱和温度之间的差值。

核沸腾

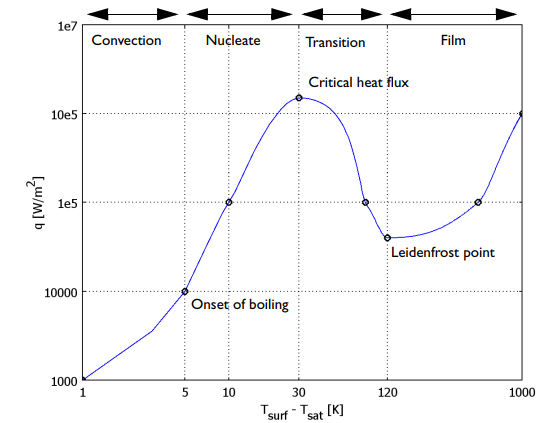
对于常压下的水，在 5 °C 到 30 °C 之间的过热度下会发生核沸腾。维持该表面温度所需的热流密度介于 \(10^4\,W/m^2\) 和 \(10^6\,W/m^2\) 之间。在这个区域中，由于固体表面缺陷所产生的成核点，会因为气相和液相之间的传质作用而发生分离和扩展。在浮力的作用下，气泡开始逐渐上升，并且可能会与其他孤立的气泡合并从而产生射流或柱状物。由于分离的气泡会迅速的被液体替代，壁面附近的液体层的有效热导率会比较高。这意味着即使施加的热流密度非常高，表面的过热度依然会比较低。核沸腾在临界热流密度时效率最高（参照图一）。在该点液体仍然可以迅速的替代产生的蒸汽，从而有效的持续润湿表面。这导致换热系数会高达\(10^4\,W/(m^2 \cdot K)\)，远远高于任何仅由对流引起的传热系数。

过渡沸腾

为了产生高于30℃的过热度，壁面吸收的热量必须降低到低于临界热流密度。这是因为一张低热导率的蒸汽薄膜开始将固体壁面与液体隔绝，降低了液体和固体壁面之间的传热系数。这个区域被称为过渡沸腾，因为在核沸腾和薄膜沸腾区域之间存在连续的局部振荡。

薄膜沸腾

为了维持薄膜沸腾，过热度和施加的热流密度必须大于Leidenfrost点。对于常压下的水。相应的热流密度需要为\(4 \cdot 10^4\,W/m^2\)左右，过热度为120K左右。一层蒸汽层持续地将加热表面与液体隔绝，并周期性地从汽液界面脱落汽泡。不像核沸腾和过渡沸腾，薄膜沸腾在本质上相对稳定并且更容易去模拟。超过Leidenfrost点后，热流密度的增加直接导致过热度的增加。在非常高的过热度下，热传导不再是加热表面到液体之间的主要传热机制，辐射的影响也必须被考虑。

图一展示了对于三种沸腾状态，施加的热流密度与过热度之间是如何变化的。当热流密度和过热度低于沸腾起点时，为自然对流。

模型定义

问题陈述

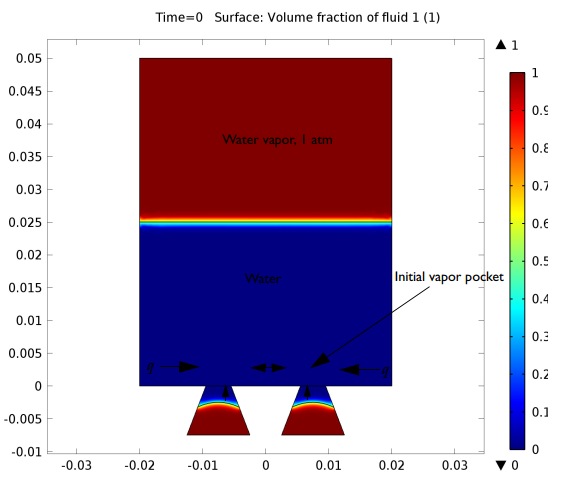
沸腾流动问题的几何和初始条件如图2所示。最初，在水箱底部的两个加热腔中，每个腔中都有水蒸气。这导致了当施加的热量大于Leidenfrost点时，稳定的薄膜沸腾发生。

模型中施加了\(10^5\,W/m^2\)的表面热流密度，这高于Leidenfrost点。为了维持薄膜沸腾，表面上的过热度预计在600K左右(总温度1000K)。

问题表述

沸腾流动的物理现象是由界面动力学来驱动的。相应的控制方程为标准Navier-Stokes方程和对流/传导方程。然而，边界条件是相当复杂的，因为液体和蒸汽之间的界面是运动的。首先，用精确的方程和边界条件描述沸腾流动问题。然后，进行了一系列近似，使得问题可以在固定网格上求解，其中界面由相场方程进行跟踪。

控制方程

液相的流场和压力由不可压缩的Navier-Stokes方程描述：

$$
\rho_L \frac{\partial \mathbf{u_L} }{\partial x}+ \rho_L\left (\mathbf{u_L} \cdot \nabla \right ) \mathbf{u_L} =\nabla \cdot \left [ -\rho _L \mathbf{I} +\mu _L\left ( \nabla \mathbf{u_L} +\left (\nabla \mathbf{u_L} \right )^T \right ) \right ] +\rho _Lg
$$

$$
\nabla \cdot \mathbf{u}_{\mathrm{L}}=0
$$

其中\( \rho_L \)为流体密度（\( kg/m^3 \)），\( \mathbf{u_L} \)为流体速度（\( m/s \)），\( \mu _L \)为